前言

前面談完 Search 之後，我們也進入老生常談的部分，也就是排序，本章節要講的是初等排序的 Insertion sort，在吸收排序這些章節的時候，要特別注重時間複雜度。此外，我們先介紹一些簡單的術語，之後在談論這些性質的時候就不多作解釋囉

Stable v.s Unstable

如果擁有多個相同鍵值的 Data，e.g. 3,2,5,2' 要求排序的話
經過排序之後，2依舊在2'前，便稱為Stable sort e.g 2,2',3,5
經過排序之後，2'跑到2前，便稱為 Unstable sort e.g 2',2,3,5
(註) unstable 雖有一些不必要的交換，如 Quick sort 為 unstable，但時間表現很好，因此 stable 和 unstable 跟時間複雜度沒有關係，這邊要注意一下唷

Insertion Sort 觀念

從 i = 2 to n 進行排序 (第1筆不用排，因為他的前面沒有人可以去比較了)
將第 i 筆資料插入 i-1 筆資料的 Sorted list 形成具有 i 筆資料的Sorted list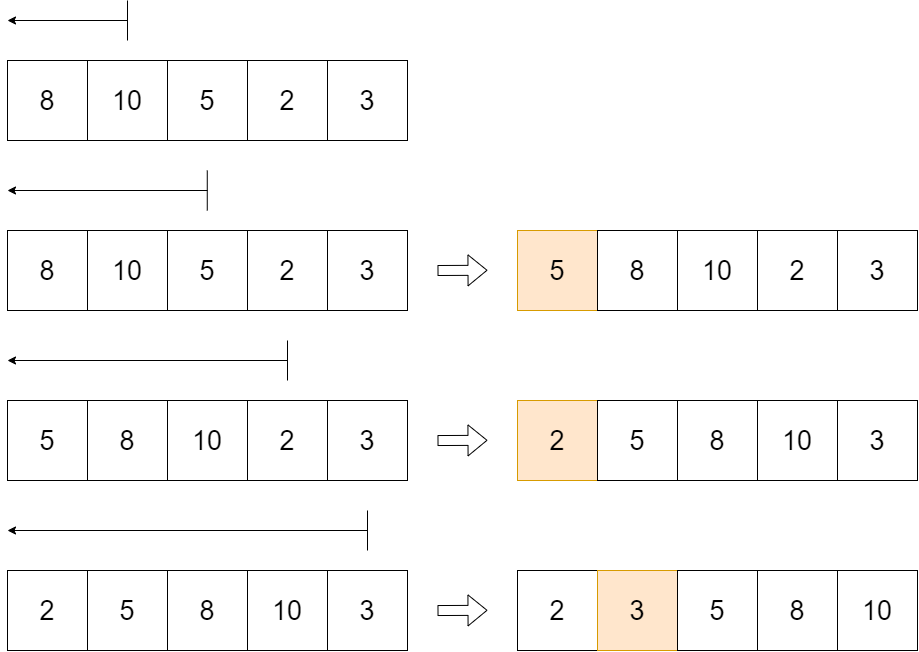

演算法

因為 array= 0…n，此外我們讓 a[0] = -inf，用來防止插入最小值進入無窮迴圈的狀況，就能簡單利用上面的觀念來寫演算法

insertionSort(){
    for i=2 to n{
        insert(a,a[i],i-1); // a is array
    }
}
insert(a, input, i){
    int j=i;
    while(input < a[j]){
        a[j+1] = a[j]; // 把比較大的元素往後挪
        j-=1; // index 往前比
    }
    a[j+1] = input; // 最後會比較到 a[0] 之 -inf，所以要 +1 放到 a[1]
}

時間分析

Best case(本來就Sorted) : O(n)，每次進迴圈只需比一次就結束，共作n-1次
worst/Avg case : O(n^2)

Stable or Unstable ?

讓我們看到演算法的這行 while(input < a[j])
當我們在進行交換的時候，必須要小於才會進行交換，因此我們來看一下下圖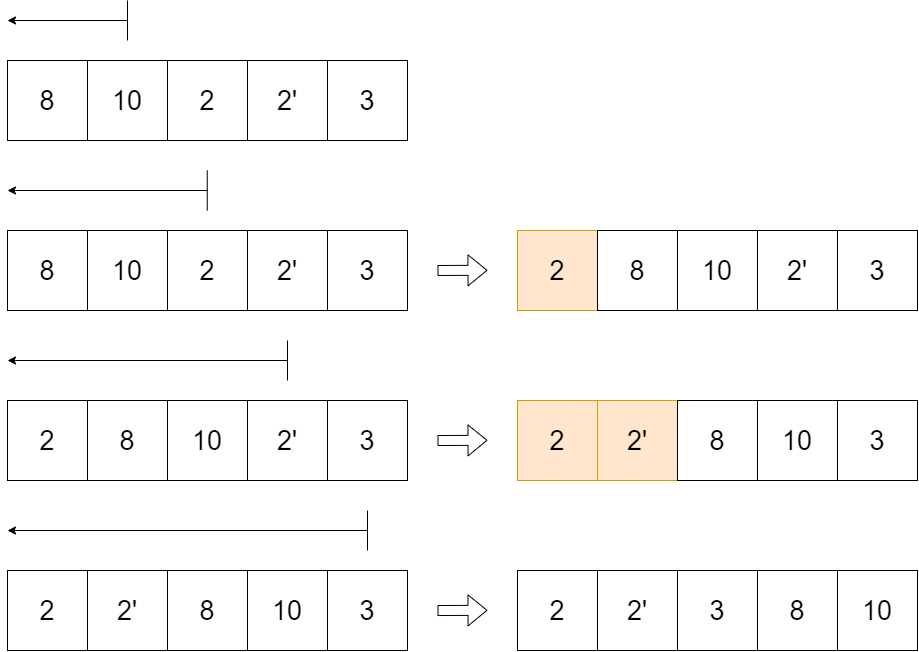

因此我們可以確保 2 一直都在 2' 前面，所以是 Stable

P.S 不要把它改成 <= 然後說他是 Unstable，安餒美塞